Turbulence:
the Lagrangian approach
I am interested in the transport properties of turbulent flows. These properties are naturally related to the trajectories of fluid particles that are advected by the flow. Recording such particles trajectories in a turbulent flow is a challenge. Indeed turbulent flows are characterized by a wide range of length and time scales. For instance, flows in laboratory scale experiments in water are usually fast (fluid velocity of the order of 1 m/s) with time scales of the evolution of the fastest eddies down to milliseconds. We use several techniques for such measurements: ultrasound and Laser Doppler techniques (that measure the velocity) or ultrafast imagery for 3D tracking of the particle’s position. With these techniques, we study the dynamics of fluid particles to get some insight in the transport and mixing properties of turbulent flows. We are also interested in the dynamics of inertial particles, i.e. particles whose density is not matched to that of the fluid. Denser particles are typically aerosols in air. The lighter particles can be gas bubbles in a liquid. Such studies are concern the elementary processes of aerosol transport in the atmosphere, sediment transport in rivers, powder catalyst in chemistry, bubble flows in water treatment facilities...
High Reynolds number turbulence in a von Kármán flow: homogeneous turbulence
A way to generate a strong turbulence in a small size experiment in a laboratory is the so called von Karman flow: water is stirred by counter-rotating turbines. On the picture on the right the turbines can be seen on top and bottom of the green cylinder (green light comes from a YAG laser). The turbines are moved by two motors at the very top and bottom. This configuration has been used a lot for fundamental studies of 3D turbulence specifically for Lagrangian studies because this flow is very turbulent (much more than a wind tunnel in air) and it is a closed flow. This flow has also been used for MHD and dynamo studies (see MHD section). For Lagrangian studies, we mark individual fluid particles by using small solid fluorescent polystyrene particles. We can then measure the trajectories in 2D or 3D by using a set of high speed cameras. In the vicinity of the center of the flow, the turbulence can be considered (to some extent...) to quite close to homogeneous (although obviously there is a stagnation point).
Lagrangian statistics in inhomogeneous turbulent flows.
Although the study of the statistical properties of particle dispersion in homogeneous turbulence led to exciting new results, real flows can rarely be considered as homogeneous due to average flow (shear) and confinement by walls. Therefore we are now studying canonical inhomogeneous, anisotropic flows: the turbulent jet and the turbulent channel flow. In such flows, the statistical analysis is made much more complex by the inhomogeneity as all statistics have to be conditioned on the position. This requires to take much bigger datasets.
The turbulent channel flow (with N. Stelzenmuller, in collaboration with I. Vinkovic and J.I. Polanco, Lyon)
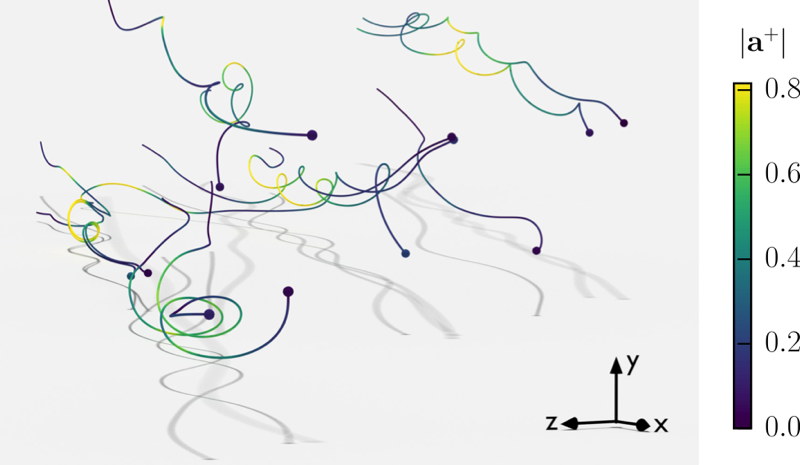
The planar turbulent channel flow is a canonical flow that is confined but still retains many symmetries. The parametrisation of the inhomogeneity requires only to conditioned on a single scalar parameter: the distance to the wall. We developed an experiment in water. I. Vinkovic and J.I. Polanco in Université Lyon 1 performed pseudo-spectral direct numerical simulation at the same Reynolds number (Re_tau=1400) that allowed us to have direct comparison between experiment and DNS. The image below shows a few trajectories from the DNS. The x-axis is streamwise and the y-axis is normal to the walls. The shadows are projected onto the wall. The color reproduce the acceleration.
The turbulent jet is a canonical flow for free shear flows. Our first experiments were using in air as the fluid. Performing particle tracking in air is challenging due to the difficulty to mark fluid particles. In, LEGI, C. Baudet and M. Bourgoin used soap bubbles inflated with Helium to match the density of air. The movie below show the soap bubbles entrained in a turbulent jet. The jet comes from the back of the movie. The light of the projector is reflected twice on each particle and the color comes from the thickness of the soap wall.
Gallery
overview of the von Karman experiment. The flow is lightened by a YAG laser sheet from the right
Close up picture of the flow seeded by 10 micron fluorescent particles (rhodamine) excited by a YAG laser sheet.
A colored filter has been used here to show isolate the red fluorescence from the green blackground
Picture of 10 micron fluorescent particles (rhodamine) excited by a YAG laser sheet, in the flow above.
View through the window. No colored filter has been used here as opposed to the picture below.
The field of view is about 2 cm which corresponds roughly to the integral scale of the flow. The exposure time is 1/250 s.
Similar view with the red filter
Movie of the 10 micron fluorescent particle. View through the red filter.
The movie has been slowed down 4 times.
